基于分层聚类图的大规模近似最近邻搜索（HCNNG）学习笔记

Posted on In

引言

最近看了一篇论文，名为：Hierarchical Clustering-Based Graphs for Large Scale Approximate Nearest Neighbor Search，总的来说这篇论文的创新点是值得学习的，但是论文对很多细节内容没有描述清楚，这也是我读这篇论文有些失望的地方（自己比较菜，所以细节问题不能详细描述的话，我很难理解的）。

这篇论文主要有两个创新点，分别为构图算法和搜索算法，构图算法采用了一种叫做多重分层聚类方法，具体这种方法有什么优势，作者没有分析；搜索算法采用了一种叫做导向搜索的方法，我们知道，几乎所有的基于图的搜索算法的搜索过程都是采用贪婪搜索，贪婪搜索的每一步要对途径点的所有邻居计算它们到查询点的距离，如果对每一个途径点能少计算一些距离，又能保证搜索结果相同，这必然会提升搜索性能，导向搜索便是如此。

构图算法

论文中的图构建过程主要分两步，分别为多重分层聚类过程和各集簇图的融合。

Hierarchical clustering procedure

多重分层聚类过程伪代码

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
Function HierarchicalClustering(P, n)
	Data: data points P, min size of clusters n
	Result: graph edges E
	N ← | P | 
	E ← φ
	if N < n then
		E ← MST3(P)
	else
		select randomly p1 and p2 points from P
		P1 ← { p ∈ P | D (p, p1 ) < D (p, p2 ) }
		P2 ← { p ∈ P | D (p, p1 ) ≥ D (p, p2 ) }
		E1 ← Hierarchical Cl ustering(P1 , n )
		E2 ← Hierarchical Cl ustering(P2 , n )
		E ← E1 ∪ E2
	return E

简述：输入数据集点集 $P$ 和集簇的最大尺寸 $n$ ，输出经过分层聚类添加的边 $ E$ （初始化 $E$ 为空）；如果输入数据集的大小 $N < n$ ，则直接在 $P$ 上通过最小生成树的变体连边（最大度为3，即 $MST3$ ）；否则，从 $P$ 中随机选两个点 $p_1$ 和 $p_2$ ，根据到其它点到这两点距离将数据集 $P$ 划分为两簇，对这两簇分别递归地执行分层聚类过程直到每个簇的尺寸都小于 $n$ 。

Fusion of graphs

各集簇图的融合的伪代码

1
2
3
4
5
6
7
8
Function CreateHCNNG(P, m, n)
	Data : data points P , number of random clusterings m , min size of clusters n
	Result : graph edges E
	E ← φ
	for i ← 1 to m do
		E i ← HierarchicalClustering(P, n )
		E ← E ∪ E i
	return E

简述：输入数据集点集 $P$ 、随机聚类数 $m$ 和集簇的最大尺寸 $n$ ，输出经过多次分层聚类添加的边 $ E$ （初始化 $E$ 为空）；对整个数据集重复分层聚类 $m$ 次，$m$ 次分层聚类得到的边都并到一起。

总结分析：在数据集上只分层聚类一次，得到的图肯定是高度不连通的，因此，要执行多重的随机分层聚类过程并连接他们的结果图。

注：本文采用分层聚类过程而没有采用K-means聚类原因是：如果事先不知道数据的分布情况，很难估计簇的初始数量和迭代次数。

搜索算法

导向搜索 VS 贪婪搜索

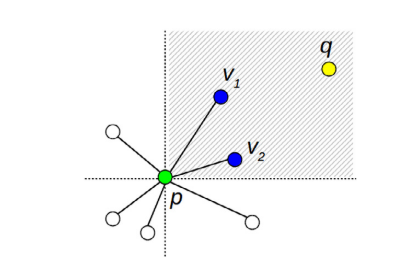
如上图所示，在搜索过程中遍历到的点 $ p$ ，贪婪搜索要计算它的所有邻居到查询点 $q$ 的距离，而导向搜索只需要计算与点 $q$ 处于同一象限的邻居。

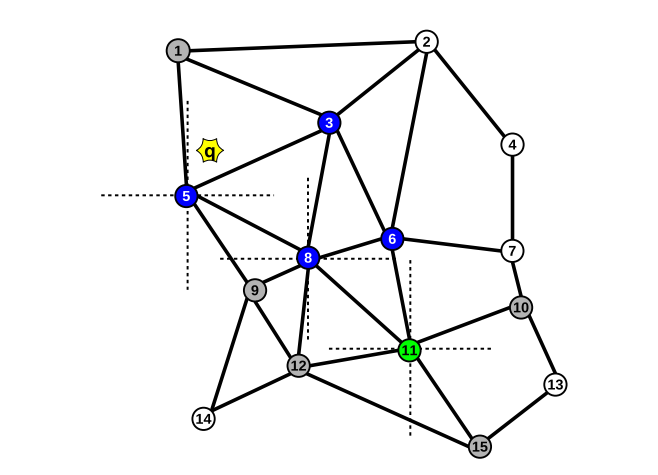
上图中传统的贪婪搜索从入口点到查询终止需要计算10次与查询点的距离，而导向搜索只需要计算5次。

导向搜索

要实现导向搜索，需要对数据集中的每个点和它的邻居创建树状结构，创建索引的时候为每个结点划分子空间，导向搜索时还要有获取与查询点处于同一象限的邻居的过程。

Creation of a tree structure to search in subspaces

主要思想：

对于已经建立的图上的某点 $p$ ，它的邻居将以树状的结构存储。在这个树状结构中，除了根结点 $p$ 和叶子结点（所有的叶子结点包含了 $p$ 的所有邻居），其它内部结点只是存储了用来划分空间的维度值（用的哪一维来划分的空间）；对于某个内部结点，它存储了某个维度值，它的两个子树是根据该维度值划分的，怎么划分呢？拿处于这个子空间的所有邻居在该维的值与点 $p$ 在该维的值比较，值小于 $p$ 的邻居被划分到 $neg$ 子树，值不小于 $p$ 的邻居被划分到 $pos$ 子树，然后再分别对这两个子树重复上述过程的划分直到对某个子树（子空间）按某维划分时得到的两个子树其中一个为空为止，此时就不用再建立存储该维的内部结点了，直接将该子树作为叶子就行了。

根据维度划分，但是这个维度怎么选呢？维度选不好的话可能建立的这个子树只是一个线性表了，这样的话建立这个树状结构就没意义了，为此要好好地选，建立的树要尽可能的保证平衡，这就要求每次选维度时要看看它是否能尽可能地等分子空间的邻居。

划分子空间伪代码

1
2
3
4
5
6
7
8
9
10
11
12
13
Function DivideSubspace( p, Np )
	Data : point of graph p, neighbors points Np
	Result : space partition tree T
	dim ← select dimension based on Np
	neg ← { v ∈ N p | v [ dim ] < p[ dim ] }
	pos ← { v ∈ N p | v [ dim ] ≥ p[ dim ] }
	if | neg| = 0 or | pos | = 0 then
		T .points ← Np
	else
	T .dim ← dim
	T .neg ← DivideSubspace (p, neg)
	T .pos ← DivideSubspace (p, pos )
return T

随记：为了实现导向搜索，在已经建好的图上对每个结点和它的邻居都建立一个树状结构（相当于附加了一个结构），这将提升搜索性能，但是会增加索引构建时间和内存占用。

Identification of neighbors at the same subspace of the query

主要思想：

在搜索的过程中，对于遍历到的某点 $p$ ，要获取其与查询点 $q$ 处于同一象限（二维情况，高维类似）的邻居，需要从根节点（点 $p$）开始一直遍历到叶子结点，遍历过程中遇到内部结点时（要确定下一步走哪个子树）将点 $q$ 在该维的值与内部结点的值进行比较以确定下一步走哪个子树，走到叶子结点时，把其中 $p$ 的所有邻居返回（这就是找到的与 $q$ 处于同一象限的邻居）。另外，这个过程消耗的时间微不足道。

获取特定邻居伪代码

1
2
3
4
5
6
7
8
9
10
11
12
Function GetNeighbors( q , p, node )
	Data : query point q , point of graph p, node of space partition tree node
	Result : neighbors in query's subspace Nq
	Nq ← φ
	if node is a tree leaf then
		Nq ← node.points
	else
		if q [ node.dim ] < p[ node.dim ] then
			Nq ← GetNeighbors (q, p, node.neg)
		else
		Nq ← GetNeighbors (q, p, node.pos )
	return Nq

构建搜索的大致过程

  1. 进行一定次数的分层聚类过程来建近邻图（在每个簇中用 $MST3$ 的方法连边，与Wang2012类似）
  2. 为建立的近邻图中每个结点和其邻居建立树结构
  3. 创建一定数量的 $KD-Tree$ （内部结点为维数），从这些树中返回的结点中寻找离查询点最近的结点作为入口点
  4. 从入口点执行导向搜索（返回的邻居中找不到离查询更近的，还可转向相邻的叶子结点）

参考文献

[1]Javier Vargas Muñoz,Marcos A. Gonçalves,Zanoni Dias,Ricardo da S. Torres. Hierarchical Clustering-Based Graphs for Large Scale Approximate Nearest Neighbor Search[J]. Pattern Recognition,2019,96.

稀罕作者