M2LSH：基于LSH的高维数据近似最近邻查找算法-阅读笔记

论文题目

M2LSH：基于LSH的高维数据近似最近邻查找算法

相关信息

作者与单位

李 灿，钱江波，董一鸿，陈华辉；

宁波大学信息科学与工程学院

出处与时间

电子学报；2017年6月

作者拟解决的主要问题

虽然位置敏感哈希(LSH)算法在解决高维空间中近邻问题上取得了非常瞩目的成就，但在处理高维数据时却很少考虑分布不均的情况。在LSH算法的基础上，本文针对高维数据分布不均的情况，提出了一种新的解决方案。

论文主要研究内容

本文提出了一种新的基于LSH的解决方案(M2LSH, 2 Layers Merging LSH)，研究内容总结：

1. 哈希方法如何应对数据分布不均匀的情况。

论文使用的方法

首先，将数据存放到具有计数功能的组合哈希向量表示的哈希桶中，然后通过二次哈希将这些桶号投影到一维空间，在此空间根据各个桶中存放的数据个数合并相邻哈希桶，使得新哈希桶中的数据量能够大致均衡。查询时仅访问有限个哈希桶，就能找到较优结果。具体如下：

索引构建

对应于一个数据集可能有多个哈希表，下面是单个哈希表的构建过程。

1. 一个数据对象$o$，经过$k_1$个距离敏感哈希函数$(h_1,\cdots, h_{k_1})$的映射，得到$o$对应的组合哈希向量$(h_1(o),\cdots,h_{k_1}(o))$，它也是$o$应放入的哈希桶号。（第一次哈希）
2. 使用$k_2$个哈希函数将$(h_1(o),\cdots,h_{k_1}(o))$投影到$k_2$条线上，使相邻的哈希桶号投影到相邻的位置。（第二次哈希）
3. 对二次哈希后组合哈希向量表示的桶号进行桶合并。合并时需要考虑3个因素：①桶中存放数据的平均数(AC)；②哈希到相邻位置的哈希桶号之间的距离；③当前哈希桶中保存数据的个数。

图1 M2LSH索引构建

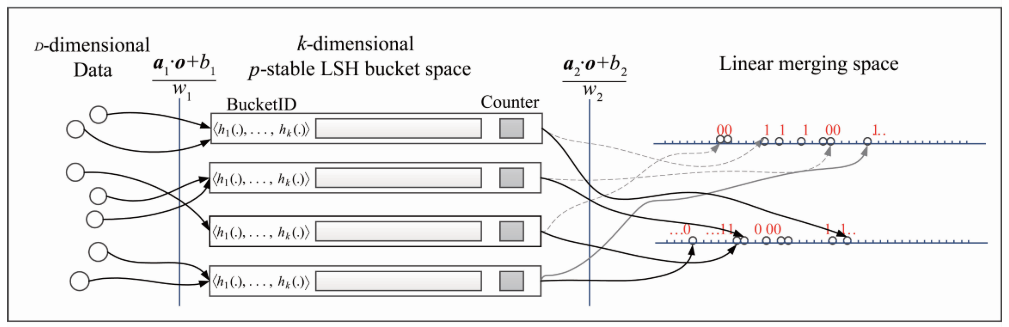
查询过程

下面是查询点$q$在一个哈希表中的查询过程。$q$经过第一次哈希后生成组合哈希向量，对其进行二次哈希后，可以知道它在直线上所映射的位置，这样只需要在直线上左右探测与其标记相同的其它桶号，那么这些桶中的数据对象也将作为$q$的查询候选集。

图2 M2LSH查询过程

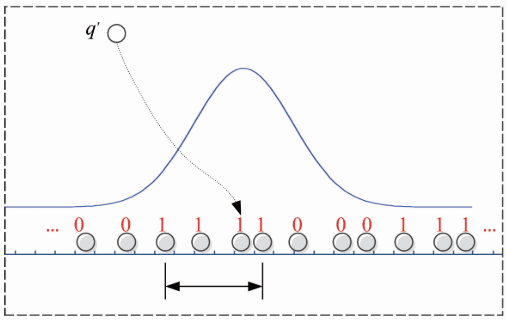
论文的创新点

为了加快查询速度，采用了对第一次组合哈希后的组合哈希桶号进行二次哈希来找与该桶相近的其它桶的策略。并且在基于桶计数以及在实际的查询中需要返回的查询结果的数量提出了哈希桶合并的方式，使得最终索引文件中每个桶中的数据个数比较均衡。

论文的结论

实验表明，M2LSH的性能要优于参与比较的方法(C2LSH; Multi-probe LSH)，特别是当数据分布不均时，M2LSH的优势更显著。

相关内容学习

本文对ANNS解决方案的总结

1. 降维。先将高维的数据映射到一个较低维度的空间，然后根据已有的低维解决KNN问题的一些方法来建立索引结构。降维后一般使用基于树的空间划分方法。
2. 编码。在计算机视觉领域的研究比较活跃。这些方法大多假设内存足够储存数据集和索引，将高维数据重新编码为一个位串，然后通过计算这些位串与查询对象之间的AQD(Asymmetric Quantizer Distance)，返回与查询对象 AQD最小的数据作为结果。
3. LSH。利用一系列具有“位置敏感”性质的哈希函数，把在空间中“比较接近”的数据对象以较高的概率映射到相同的哈希桶中。

我的观点或思考

本文从LSH的角度应对数据分布不均的问题，并没有对数据集分布不均问题做通用的处理。传统的LSH方法面对分布不均的数据时会存在这样的缺陷：某些桶中数据对象非常多，而另一些桶中数据对象又非常少，此时会使相应的LSH方法的性能很不稳定。本文经过二次哈希以及桶合并缓解了这一问题。