NN-Descent构建K近邻图——论文超详细注解

论文题目

Efficient K-Nearest Neighbor Graph Construction for Generic Similarity Measures

作者拟解决的主要问题

K近邻图的构建在很多基于Web的应用上是一个重要的操作，比如协同过滤（基于用户的邻居作推荐）、相似性搜索等。一个有效地构建方法将使K近邻图的应用更加广泛。

暴力构建K近邻图的时间复杂度为$O(n^2)$，为了能更高效的构建K近邻图，现存的工作扩展性都不太好，而且一般都特定于具体的相似性度量。

有效的K近邻图构建仍然是一个开放的问题，解决该问题的已知方案中没有一个是通用、有效和可扩展的。因此，本文提出了NN-Descent方法，该方法具有以下优点：

通用。适用于任意的相似性度量准则。
可扩展。随着数据集尺寸的增加，Recall仅有很小的下降。由于对每一个数据点的局部信息进行操作，因此适用于分布式计算环境（MapReduce）.
节省空间。整个构建过程仅涉及到一种数据结构——近邻图。
快速、精确。百分之几的相似性比较便可实现90%以上的召回率。
容易实施。主要代码不超过200行（C++）。

论文主要研究内容

如何有效地构建一个K近邻图，具体如下：

适用任意相似性度量的K近邻图构建方法。
在较短的时间内快速构建K近邻图的方法。
构建一个在其上能快速、精确执行搜索的K近邻图。
适用于MapReduce框架的K近邻图构建方案。

论文使用的方法

抽象描述注解

$V$表示数据集，数据集尺寸为$N=|V|$，相似性度量$\sigma$：$V \times V \rightarrow R$。$\forall v \in V$，$B_K(v)$表示$v$的$K$个最近邻，$R_K(v)= \lbrace u \in V | v \in B_K(u) \rbrace$表示$v$的反向K个最近邻。$B[v]$和$R[v]$分别表示$B_K(v)$和$R_K(v)$的近似。$\overline{B}[v]=B[v] \cup R[v]$表示$v$的一般邻居。

当在$V$上的度量方式为距离度量时，即$d$：$V \times V \rightarrow [0,\ +\infty]$。$\forall r \in [0,\ +\infty]$，以$v$为球心的r-球定义为：$B_r(v)=\lbrace u \in V | d(u, \ v) \leq r\rbrace$。

如果$\exists c$满足：
$$
|B_{2r}(v)| \leq c|B_{r}(v)|, \ \forall v \in V \tag{1}
$$
则称度量空间V增长受限，$c$是增长常量。

基础算法注解

基本思想：邻居的邻居更可能是邻居。

理论推导

我们可以从$V$中每一个点的现有的近似K近邻出发，通过探索该点邻居的邻居（在当前近似K近邻中）而不断完善该点的K近邻。换句话说，可从粗略的K近邻图出发通过改进而不断完善它。对这一观点的量化表达如下：

让$K=c^3$（后面公式推导要用到，$K$取此值是方便推导），假定已有的近似K近邻图（可以随机给每个点选邻居构建，也可通过其它数据结构辅助构建，如哈希，树等）为$B$。$\forall v \in V$，$B^\prime[v]=\bigcup _{v^\prime \in B[v]} B[v^\prime]$表示$v$所有邻居的邻居集合，它也是在完善$v$的K近邻时的候选点集。当B的精度比较高时（迭代完善了一定次数或通过某种更好的方式初始化B），高到什么程度呢？就是给定一个固定的半径$r$，对$\forall v \in V$，$B[v]$包含的K个邻居均匀地分布在$B_r(v)$中。这样的话，当各事件相互独立且$K<< |B_{r/2}(v)|$时，$B^\prime [v]$很可能包含在$B_{r/2}(v)$中的K个邻居。换句话说，对$\forall v \in V$，通过探索$B^\prime [v]$来使$v$到它的近似K近邻的距离减半。

对$B_{r/2}(v)$中的一点$u$，要从$B^\prime[v]$里面找到，则至少存在一点$v^\prime$，使得$v^\prime \in B[v]$，且$u \in B[v^\prime]$。接下来，我们只需要找满足上述条件的$v^\prime$即可。而若$v^\prime \in B_{r/2}(v)$，则有以下几个不等式成立：

$v^\prime \in B_r(v)$，因此，$P\lbrace v^\prime \in B[v]\rbrace \geq K/|B_r(v)|$，$P\lbrace v^\prime \in B[v]\rbrace$表示概率。注解：$v^\prime \in B_{r/2}(v)$，则$v^\prime \in B_r(v)$必然成立。若$v$的$K$个邻居都在$B_r(v)$中取的话，则一共有$C_{|B_r(v)|}^K$种情况，而$B_r(v)$中的一点不是$v$的邻居的情况有$C_{|B_r(v)|-1}^K$种，$B_r(v)$中的一点不是$v$的邻居的概率为$C_{|B_r(v)|-1}^K/C_{|B_r(v)|}^K$，即为$(|B_r(v)|-K)/|B_r(v)|$，因此$B_r(v)$中的一点是$v$的邻居的概率为$1-C_{|B_r(v)|-1}^K/C_{|B_r(v)|}^K$，即为$K/|B_r(v)|$。$B_{r/2}(v)$中的一点更可能是$v$的邻居，故$v^\prime$是$v$的邻居的概率大于等于$K/|B_r(v)|$。
$d(u,\ v^\prime) \leq d(u, \ v) + d(v, \ v^\prime) \leq r$，因此，$P\lbrace u \in B[v^\prime]\rbrace \geq K/|B_r(v^\prime)|$。注解：由第一条推论可知，因此$B_r(v^\prime)$中的一点是$v^\prime$的邻居的概率为$K/|B_r(v^\prime)|$，而$u$与$v^\prime$的距离小于等于$r$，故$u$是$v^\prime$的邻居的概率大于等于$K/|B_r(v^\prime)|$。
$|B_r(v)| \leq c|B_{r/2}(v)|$，且$|B_r(v^\prime)| \leq c|B_{r/2}(v^\prime)| \leq c|B_r(v)| \leq c^2|B_{r/2}(v)|$。注解：重点是$|B_{r/2}(v^\prime)| \leq |B_r(v)|$部分的推导，而此处可由图1明显推出。由于$v^\prime$在$v$的$r/2$-球中，$v^\prime$的$r/2$-球一定包含于$v$的$r$-球中。

图1 不等式推导二维辅助理解图

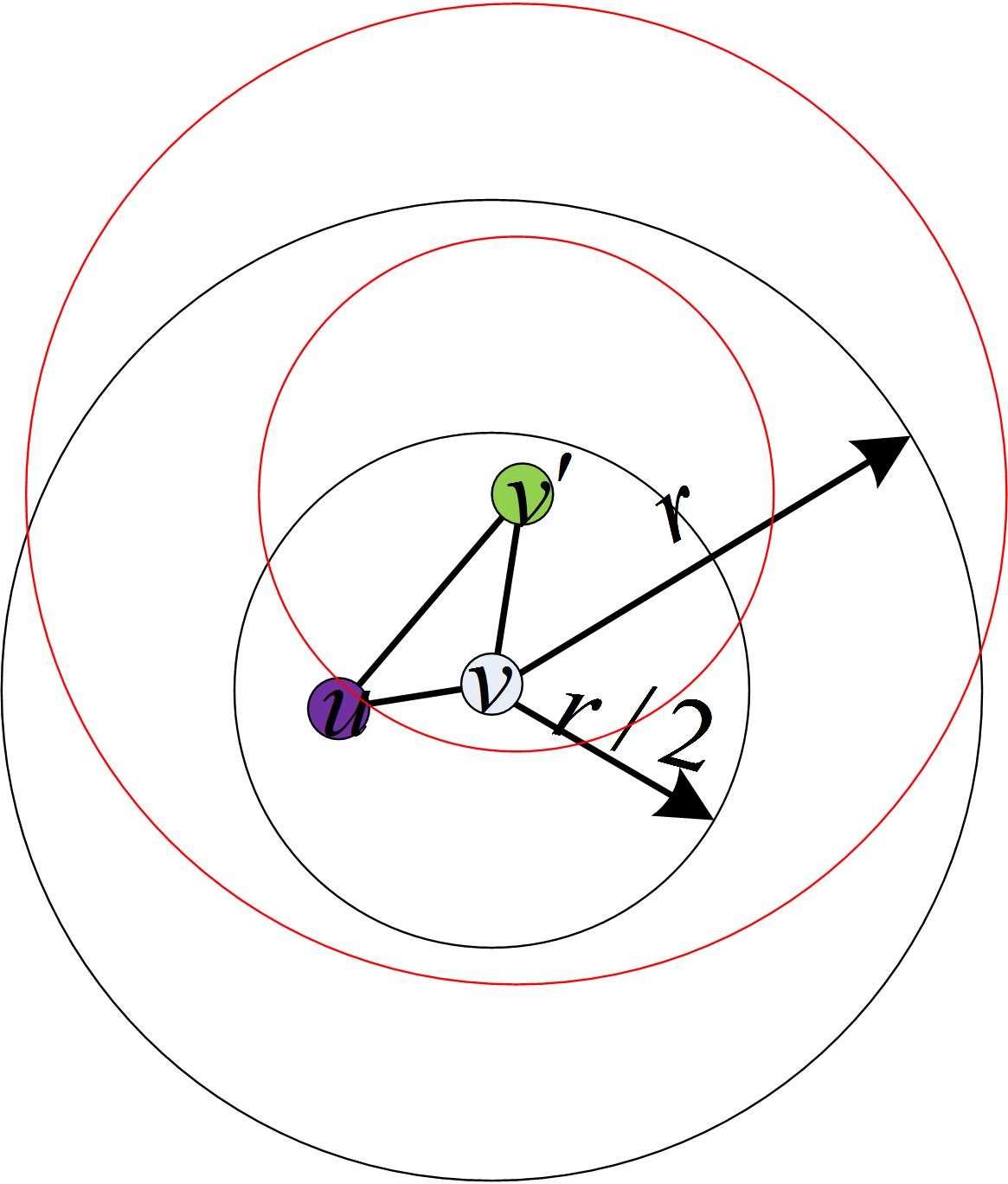
由以上3个不等式和假定的各事件的独立性可得：
$$
P\lbrace v^\prime \in B[v] \land u \in B[v^\prime]\rbrace \geq K/|B_{r/2}(v)|^2 \tag{2}
$$
注解：上式其实就是1.与2.两个事件同时发生的概率再由3.式化简的结果。它的意义是，对于$B_{r/2}[v]$中的确定的点$v^\prime$，它既是$v$的邻居又是$u$的反向邻居的概率大于等于$K/|B_{r/2}(v)|^2$。

因此，当$v$的邻居从$B_{r/2}(v)$中取时，在$B_{r/2}(v)$中的一点$u$属于$v$的邻居的邻居的概率为：
$$
P\lbrace u \in B^\prime[v]\rbrace \geq 1-(1-K/|B_{r/2}(v)|^2)^{|B_{r/2(v)}|} \approx K/|B_{r/2(v)}| \tag{3}
$$
注解：先考虑$u$不是$v$的邻居的邻居的概率。此时，从$B_{r/2}(v)$中取出的一点设为$x$，$x$不是$v$的邻居或者$u$不是$x$的邻居，发生这种情况的概率由式（2）可得应为$1-K/|B_{r/2}(v)|^2$，$B_{r/2}(v)$中一共有$|B_{r/2}(v)|$个点，它们都不满足上述情况（$x$不是$v$的邻居或者$u$不是$x$的邻居）的概率为：$(1-K/|B_{r/2}(v)|^2)^{|B_{r/2(v)}|}$，这便是$u$不是$v$的邻居的邻居的概率，从而$u$是$v$的邻居的邻居的概率为：$1-(1-K/|B_{r/2}(v)|^2)^{|B_{r/2(v)}|}$。下面对该式进行化简，由于$K<< |B_{r/2}(v)|$，因此$K/|B_{r/2}(v)|^2$是无穷小，化简过程用到一个重要极限：
$$
\lim_{x \rightarrow \infty}(1+\frac{1}{x})^x=e \tag{4}
$$
一个等价无穷小公式：
$$
e^x -1 \sim x
$$
整个数据集的直径设为$\Delta$，式（3）表明，只要我们取一个足够大的$K$（取决于增长因子$c$），即使我们从一个随机的K近邻图开始，通过探索每一个对象邻居的邻居，便可找到该对象的处于半径为$\Delta/2$的范围内的K个近邻。不断的迭代这一过程，每个对象的邻居距离该对象的距离会不断收缩，最终，构建一个高质量近似K近邻图。

伪代码

算法1 NN-Descent基础算法

注解：(1)处为更新统计，如果某一个对象的K近邻列表更新了，$c$就会加1。算法1的终止条件为自然终止，即没有更新时（$c=0$）终止。

改进算法注解

局部连接

让每一个对象探索它邻居的邻居的操作也可通过局部连接等价实现。局部连接可这样理解：给定一点$v$，它的邻居集为$\overline{B}[v]$，在$\overline{B}[v]$上的局部连接是计算每一对不同的$p$和$q$之间的相似性（$p，q \in \overline{B}[v]$），并且根据此相似性更新$B[p]$与$B[q]$。通俗的将，局部连接就是每一个点介绍它的邻居去了解彼此。

局部连接能代替一个对象探索它邻居的邻居的操作吗？看下面的示例：

图2 局部连接实现示例

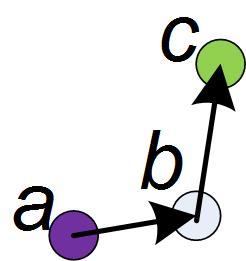
如图2所示，$b \in B_K(a)$，$c \in B_K(b)$。在算法1中，当探索到$a$时，我们需要比较$a$与$c$，当探索到$c$时，我们也需要比较$a$与$c$，这是冗余计算的一种情况，可通过索引编号的顺序来解决。同样地，$a$与$c$之间的比较可通过对$\overline{B}[b]$进行局部连接来实现。

局部连接实现起来很简单，那么它有什么好处呢？

增强了数据的局部性，使执行更有效。如果每一个对象的邻居的个数平均为$\overline{K}$，算法1每次迭代探索每一个对象的邻居的邻居时将接触到$\overline{K}^2$个点，而局部连接只需要接触$\overline{K}$个点。
单机实施时，提升了cache的命中率，从而加速了K近邻图的构建。分布式实施时，能减少机器之间数据的复制。

增量搜索

随着算法的执行，每一个对象的K近邻更新的幅度逐渐减小。而且，在某次迭代中参与比较的两个点，就更可能在之前的迭代中已经比较过了。这就造成冗余计算，而增量搜索就是要解决这个问题的。

给每一个点的K近邻列表中的每一个对象附加一个布尔标记，当一个新对象插入到该列表中的某个条目时，它的标记初始化为true。
只有当两个对象至少一个的标记为true，它们才进行局部连接。一个对象参与局部连接之后，它被标记为false（true变false，false还是false）。

采样

采样是为了解决以下两个问题：

局部连接的高成本。一次迭代，就算只考虑K近邻，时间复杂度为$K^2N$，如果再考虑反向近邻，时间复杂度更高。
冗余计算。两个点同时连接到多个不同对象，这两个点将比较多次。

使用采样来缓解这两个问题的具体方案如下：

邻居取样。局部连接之前，对用于局部连接的每一个对象，从标记为true的K近邻中取样$\rho K$个对象（$\rho \in (0, 1]$）。每一次迭代，仅仅这些被取出的数据被标记为false。
反向邻居。只根据取样对象和标记为false的对象来构建反向邻居列表。对构建得的反向邻居列表再次取样。
在标记为true对象之间进行局部连接，以及在标记为true对象与标记为false对象之间进行局部连接。

因此，我们就可以通过取样率$\rho$来进行精度和速度的trade-off。

提前终止

一个很自然的终止标准是：某次迭代中，K近邻图不再被改善。实际上，开始迭代时，K近邻图能充分的更新，而随着迭代的进行，K近邻图更新的次数快速收缩，此时的迭代就显得意义不大了，考虑到迭代的计算成本，这些迭代其实没必要执行。为了解决这个问题，本文采取的方案是：在每次迭代中，统计所有对象K近邻列表更新的次数$count$，当$count < \delta KN $时终止发生，其中$\delta$是精度参数，它粗略反应了由于提前终止允许错过的真正的K近邻的比例。

伪代码

算法2 NN-Descent改进算法

注解：算法2是在算法1的基础上结合了四个改进（局部连接；增量搜索；采样；提前终止），注意算法2其实也不能完全避免冗余计算，先理解一下这个算法，然后我会给出示例。

(1)、(2)属于增量搜索和采样部分，对于当前对象$v$，在它的邻居列表中取$\rho K$个标记为true的邻居到$new[v]$，并将这些邻居标记为false（对于伪代码中的(3)），在它的邻居列表中取出所有标记为false的邻居到$old[v]$。

(4)是取$v$的反向邻居，正如取$v$的$old[v]$一样，其它所有点也会取各自的$old$，以所有点的$old$集合中包含的点作为探索范围，检查它们的邻居列表中含$v$的点，含$v$则加入到$old^\prime [v]$，$old^\prime [v]$的意义是：点$v$的反向邻居，且在该反向邻居的邻居表中，$v$被标记为false。$new^\prime$同理。

(5)是说最后参与局部连接的$old[v]$是由两部分组成：一部分是从$v$的邻居列表中取出的标记为false的邻居集，另一部分是从$old^\prime [v]$中取样的$\rho K$个点。最后参与局部连接的$new[v]$同理（(6)）。

(7)表示局部连接。$new[v]$里面的点相互之间进行局部连接，为防止重复比较，设定比较顺序。$new[v]$中的点与$old[v]$中的点进行局部连接。

(8)统计更新，某一对象的邻居列表更新时，新插入的对象标记为true（满足：增量搜索）。

(9)为终止条件。当更新量小于某一阈值时终止。

冗余计算示例

图3 冗余计算示例

如图3所示，第一次迭代时$v_3$和$v_4$都取样了$v_1$，都没有取样$v_2$，因此，它们的邻居列表中$v_1$都标记为false，$v_2$都标记为true。此时，$new^\prime[v_1]$含$v_3$、$v_4$，若$v_3$、$v_4$都被取样加入到参与局部连接的$new[v_1]$，则$v_3$和$v_4$会进行一次相似性计算。第二次迭代时，$v_3$和$v_4$都取样了$v_2$，然后$v_2$在它们的列表中被标记为false。此时，$new^\prime[v_2]$含$v_3$、$v_4$，若$v_3$、$v_4$都被取样加入到参与局部连接的$new[v_2]$，则$v_3$和$v_4$又会进行一次相似性计算。

当然，上述分两次迭代的说明也可在一次迭代中发生。不过，上述冗余计算的情况在取样过程的参与下发生的概率是很小的。

论文的创新点

一种新的构建K近邻图的方法，具体创新包括：

对于一个随机K近邻图，通过几次迭代而不断的完善K近邻图，最终得到一个更好的K近邻图。（构图思路）
处理某个点时，在该点的各邻居之间进行选边。这种方式相较于处理某个点时，该点与该点的邻居的邻居之间进行选边而言，局部性更好。两种方式实现的结果都是一样的。（选边策略）

论文的结论

具体实验分析可以看作者的原文。本文提出的NN-Descent方法可使用任意度量方式构建的K近邻图。经验复杂度为$O(n^{1.14})$，很容易实现并行化。

我的观点或思考

本文一开始是随机构建一个K近邻图，这样做的优点是简单快速。但是，迭代的过程过多地依赖随机初始化的K近邻图，这样可能不够稳定，某些情况下只需几次迭代，而另一些情况则可能需要很多。因此，一个简单地改进可从初始化K近邻图这个角度入手。

最近提出的基于近邻图的近似最近邻搜索算法——NSG和NSSG，他们在构建索引时，第一步构建K近邻图与第二部MRNG或SSG选边策略是分开进行的，有没有可能在K近邻图构建的同时执行某一选边策略。

选边的时候将三角不等式考虑进去，从而避免一些不必要的计算。