HNSW启发式选边策略分析

为什么启发式选边？

HNSW是增量式构建的，构图时它的启发式的选边策略不仅考虑了相似度问题也考虑了数据的分布问题。因为HNSW是站在近似最近邻搜索的角度去考虑的，而不是站在构建一个尽可能精确的近邻图的角度考虑问题，这可以说是HNSW选用启发式选边的intuition。一个精确的近邻图不一定是最适合近似最近邻搜索的。

既考虑相似度问题又考虑数据分布情况的选边策略有很多，这里选用启发式选边有何优势？请看它具体是怎样操作的。

怎样启发式选边？

图1 HNSW启发式选边示意

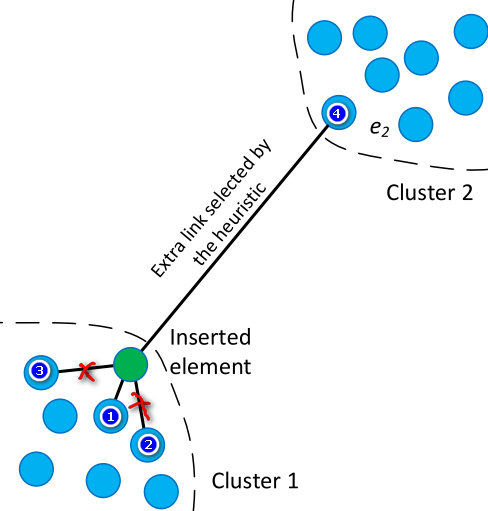
图1中绿色的点是刚插入点，假设它的候选邻居集足够大能涵盖图中所有蓝色点，假设一个点最多只能连4个邻居。根据论文中的描述，绿色点的最近邻居（图中编号为1的点）必连，接着检查第二近的邻居（编号为2），点2与绿色点的距离大于点2与点1（其实点2要与选中的点集中所有点都要比较选一个距离最小的，此时选中的点只有点1）的距离，因此点2不连（放入垃圾堆），额，图1中怎么给连上了？这是论文作者连的，误操作？这里先给它画个红叉。继续检查第3近的邻居（编号3），点3与绿色点的距离大于点3与点1的距离（可能不太明显，暂且这么认为），因此点3也不连（放入垃圾堆），又误操作？剩下的Cluster1中的蓝色点按到绿色点的距离由近及远重复执行上述操作，很明显，它们都不会与绿色点连边，统统放入垃圾堆。

因为我们的候选邻居集足够大，下面轮到Cluster2中的点了，先点4，它与绿色点的距离小于它与点1的距离（此时只选中了点1），因此选中点4，接下来Cluster2中的其它点重复上述操作都不会选中，放入垃圾堆。经过一波启发式之后，已给绿色点选了两个邻居，分别是点1和点4，但是我们需要给插入点选4个邻居，还差2个，论文中的处理很简单，从垃圾堆里面选两个离绿色点最近的连边，毫无悬念，点2和点3光荣选中，毕竟在垃圾堆里它们离插入点更近。这个时候，图1中的那两个红叉可以去掉了，误操作不存在的。

有什么好处呢？

先说一下它的一个明显的缺点，复杂了一些，肯定比只考虑距离的朴素选边策略构建复杂度更高，它多计算了一些距离。

为了更好的搜索性能，索引构建的这点小牺牲算不了什么。启发式选边的优势主要有以下两点：

尽可能地保证图的全局连通性，特别是数据集在分布上有很多聚簇时；
长边起到“高速公路”的作用，使搜索过程可以快速收敛。

先说第1点，注意关键词“尽可能地”，这里的意思是，相比朴素选边，启发式选边在某些情况能保证图的全局连通性，但不保证所有情况。下面这个例子应该能清晰说明启发式相比于朴素式的优势，前者能保证全局连通性，而后者不能保证全局连通性。

图2 HNSW插入式图构建过程简化版（不考虑分层）

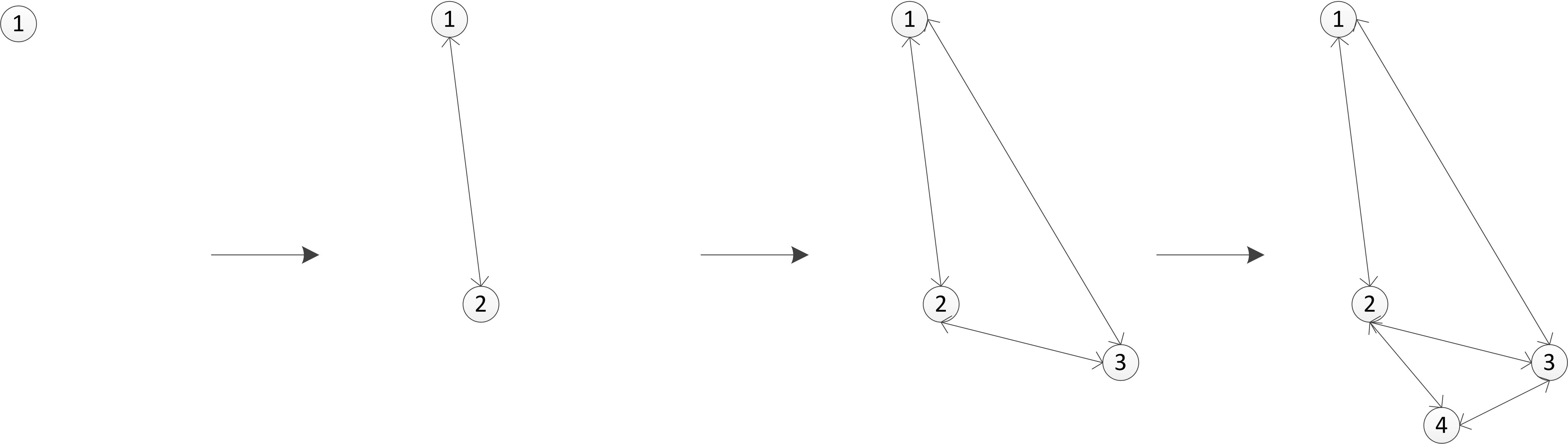
图2是HNSW简化版的插入式构图过程，假设每个点最多连两个邻居，插入过程为插入点选边也是按照启发式的策略，这里只给出结果，具体过程可自行分析，其实图2给出的例子启发式和朴素式选边的结果都是一样的。需要注意的一点是：HNSW给插入点选邻居时，在选中的邻居与插入点之间连接的是双向边，HNSW构建的是一个有向图。

插入点1，2，3都没什么问题，当插入点4后，点2和点3邻居“超载”，需要裁边。裁边的时候采用的策略也是启发式的，裁边后的结果看图3，具体过程可按启发式的过程自行分析。