根据查询需求自适应k值构建近邻图｜日本电信电话株式会社｜SIGKDD CCF A类会议

Posted on In

论文题目

Fast approximate similarity search based on degree-reduced neighborhood graphs

相关信息

作者与单位

Kazuo Aoyama
NTT Communication Science Laboratories, NTT Corporation 2-4, Hikaridai, Seika-cho,
Soraku-gun, Kyoto, 619-0237, Japan
aoyama.kazuo@lab.ntt.co.jp Kazumi Saito
University of Shizuoka 52-1, Yada, Suruga-ku, Shizuoka, Shizuoka, 422-8526, Japan k-saito@u-shizuoka- ken.ac.jp
Naonori Ueda
NTT Communication Science Laboratories, NTT Corporation 2-4, Hikaridai, Seika-cho,
Soraku-gun, Kyoto, 619-0237, Japan
ueda.naonori@lab.ntt.co.jp Hiroshi Sawada
NTT Communication Science Laboratories, NTT Corporation 2-4, Hikaridai, Seika-cho,
Soraku-gun, Kyoto, 619-0237, Japan
sawada.hiroshi@lab.ntt.co.jp

出处与时间

SIGKDD, 2011 (CCF A类)

作者拟解决的主要问题

  1. 近邻图构建时高的构建成本；
  2. 由于近邻图方法是启发式的，因此搜索的结果不清晰。

论文主要研究内容

  1. 如何从ANNS的角度定义一个图的质量；
  2. 给定数据集和查询成功概率约束，如何在其上构建一个自适应k值的近邻图；
  3. 如何降低图的出度。

论文使用的方法

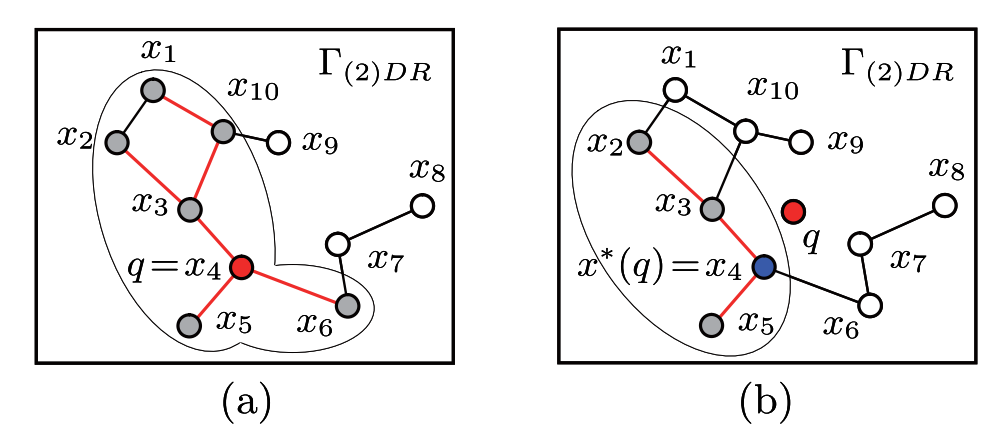
论文中提出的$Basin$（下译为：盆地）概念。盆地与查询点的位置和图的结构有关，因此，它表示为：$Basin(q, \ G)$。盆地其实是一个顶点集合，它是图中顶点的子集。从这个子集中的点出发根据贪婪搜索进行扩展必然能到达查询$q$的精确最近邻点。以盆地中的点作为起始点在图上执行贪婪搜索时不会受局部最优问题的影响。图1是同一个图上两个不同位置的查询对应的盆地（(b)中的$x_6$也应该包含在盆地中吧？）。



图1 环包围的点构成盆地

图构建

本文图构建过程分两种情况，一种是k确定；另一种是k先前不确定。第一种比较简单，本文通过增量的方式构建，大意是先构建1近邻图，接着2近邻图，。。。，直到k近邻图。而且，在添加无向边时，还要先判断两个点之间是否可通过贪婪搜索可达，若是，则不连边，否则，连。

论文重点介绍了k先前不确定的情况，这也更符合实际应用。这里会用到基于$Basin$定义的贪婪搜索查询成功的概率。构建过程也是增量进行的，重要的一步是每次增量前要先判断当前已构图是否达到给定的贪婪搜索成功的概率。是否添加边也同k固定的情况一样先判断是否通过贪婪搜索可达。

并行贪婪搜索

比较普通的贪婪搜索过程。可以多个起始点并行进行。作者还给出了有范围约束的贪婪搜索版本。

论文的创新点

提出一个$Basin$概念，并基于此给出了贪婪搜索算法在一个图上找到给定查询精确最近邻的成功概率的计算公式。

论文的结论

  1. k值越大，$Basin$的尺寸越大；
  2. 本文图构建的时间复杂度为$O(n^2)$；
  3. 在预期的搜索成本下，实现一个给定的召回率，本文提出的方法与之前方法相比具有优势。

我的观点或思考

  1. 本文提出的k-DR图是对k近邻图的近似，并且它还具有小世界性质。
  2. 本文提出的$Basin$概念引申出来的贪婪搜索成功的概率是否可以作为近邻图ANNS算法性能指标的一部分呢？文中计算贪婪搜索成功的概率稍微复杂一些，如果从简考虑是不是可以取一个比较小的数据集，在其上构图后，通过线性扫描的方法计算盆地。
稀罕作者