引言
最近,基于近邻图的近似最近邻搜索算法(ANNS)取得了最优的效率和精度权衡。在图索引上,路径的单调性对相关ANNS算法的搜索性能起着至关重要的影响。几种当前最优的ANNS算法比如HNSW,NSG普遍能使搜索路径尽可能的单调递减,从而避免由于“绕远路”而降低搜索效率。本文介绍的几种proximity graphs是这些ANNS算法的基础,与当前的实用算法相比,这些proximity graphs有着严格的形式化定义,这给理论分析相关性质带来便利,从而也给实用的ANNS算法提供理论保证和优化方向。接下来,我们主要分析proximity graphs的单调性,proximity graphs包括德劳内图(Delaunay Graph, 它与voronoi diagram对偶)、Relative Neighborhood Graph (RNG)、Gabriel Graph (GG)、Minimum Spanning Trees (MST)。
首先给出结论:Delaunay Graph 是单调的图,而RNG, GG和MST都不是单调的图。
何为图的单调性
在此之前,我们需要先了解一下什么是单调路径?对于图G上的一个m个依次邻接的顶点形成的路径$(v_{1},v_{2},\cdots, v_{m})$,若$dist(v_1,v_m) > dist (v_2, v_m) > \cdots > dist(v_{m-1},v_m)$,则该路径是一条单调路径,$dist(,)$表示两个顶点之间的距离。如果一个图G的任意两个顶点之间均存在单调路径,则图G便是单调图了。
如何证明一个图不是单调的
只需要举一个反例就行了。任意画几个点,分别根据RNG, GG和MST的定义建立相应的图结构,很容易找到不存在单调路径的例子。
证明DG是单调的
下面证明DG是单调的。在此之前先给出一个定理。
定理1. 对于DG中的任意两个顶点$v_a$和$v_j$,存在一个德劳内边$e_{ak}$满足$d(v_k, v_j) < d(v_a, v_j)$。
证明:给定在数据集S上的DG。$v_a$可能在DG的边界(如图1(a))或在DG的内部(如图1(b))两种情况。但无论哪一种情况,$v_a$对应的Voronoi diagram(图1中虚线围成的绿色多边形区域,记为$V(v_a)$)都不包含其它点(这是由定义保证的),所以$v_j$一定落在$V(v_a)$外面。因此,连接$v_a$和$v_j$的线段一定经过$V(v_a)$的至少一条边。记这条边为$e_{ak}$的垂直平分线$h_{ak}$,$v_j$和$v_k$在$h_{ak}$的同一侧,故$d(v_k, v_j) < d(v_a, v_j)$。
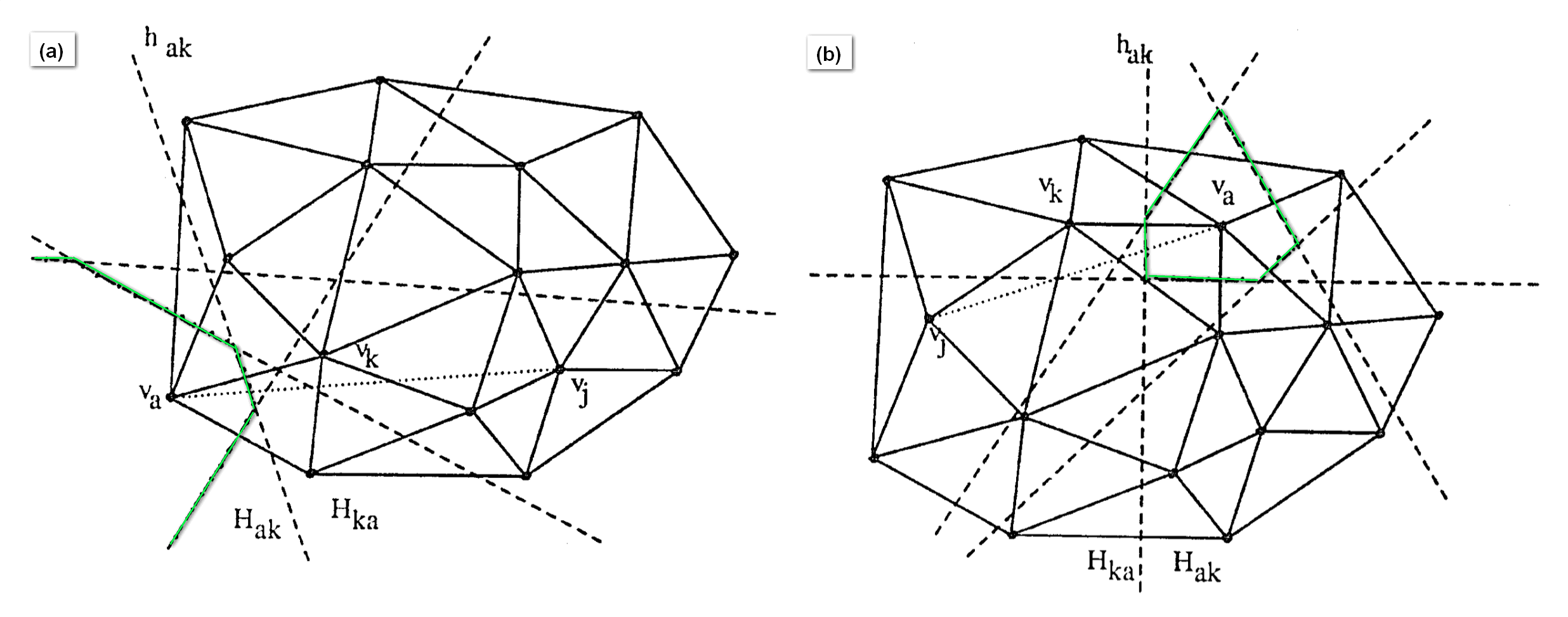
下面证明DG是单调的。
证明:我们只需证明DG中的任意两个点$v_a$和$v_j$,总存在一条由$v_a$至$v_j$的单调路径。若$v_j$是$v_a$的邻居,则单调路径是显然的。接下来,我们考虑$v_a$与$v_j$不邻接的情况。根据定理1,存在一条边$e_{ak_1}$,满足$d(v_{k_1},v_j) < d(v_a,v_j)$,存在边$e_{k_{1}k_2}$,满足$d(v_{k_2}, v_j) < d(v_{k_1},v_j)$ … …,最终,存在边$e_{k_ij}$,满足$d(v_j, v_j) < d(v_{k_i)},v_j)$。从而路径$(v_a, v_{k_1}, \cdots,v_{k_i},v_{j})$满足$d(v_a, v_j) > d(v_{k_1}, v_j) > d(v_{k_2},v_j) > \cdots > d(v_{k_i},v_j) > d(v_j, v_j)$,即是一条单调路径。
RNG几乎是单调的
虽然不能确保RNG是单调的,但在大部分情况下RNG是单调的,而且RNG是几乎所有单调图的子图。
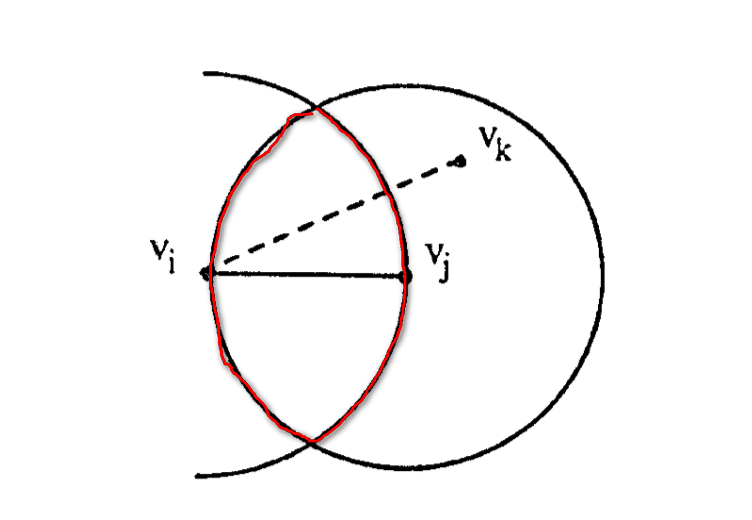
如图2所示,边$e_{ij} \in$ RNG,则$lune(i,j)$(红色圆弧包围的部分)是空的,即里面没有其它点(RNG的定义决定的)。因此,一条从$v_i$至$v_j$且不包含$e_{ij}$的单调路径的中间点必然落在红色圆弧上,即图3所示的$v_{k_1}$。
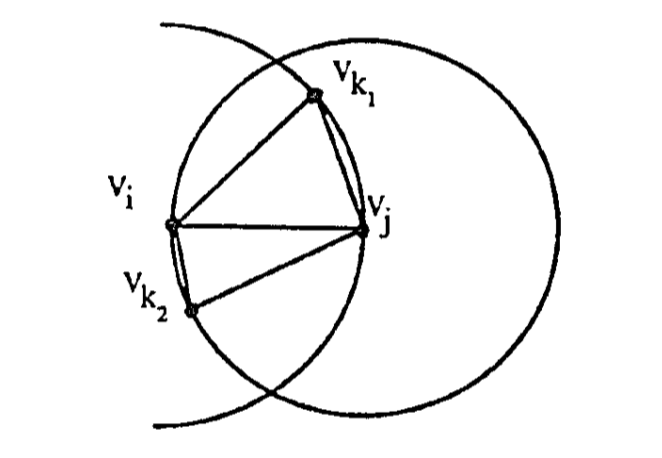
在图3中,$(v_i, v_,v_j)$是单调路径,此时,$e_{ij}$就是冗余边,因为可通过其它单调路径由$v_i$到$v_j$。因此,就RNG而言,若存在冗余边,则可替代单调路径的中间点必须落在图2的红色圆弧上,发生这种情况的概率是非常小的。
参考文献
Kurup, G. D. (1992). A database organized on the basis of similarities with applications in computer vision.

