论文概述
相似性搜索是计算机视觉的一个基础模块。早期,一个图像将会对应几千个向量,因此,使用compact representation非常重要。最近,一个图像对应一个向量(通常从卷积神经网络的激活层提取)。
本文大致思路:(1)通过OPQ 压缩原始向量;(2)根据邻居执行量化回归不断优化量化码。通过交替优化学习一个回归码本(该码本即为通过离一个点的最近的几个点重构该点时的权重系数或回归系数或重构系数)以最小化重构误差。
贡献:
- 近似一个点时,粗质心比最近邻效果更好。向量能被它的少量邻居的线性组合(带有固定混合权重)更好的近似,如果能存储每一个向量的权重,效果会更好;
- HNSW比基于倒排列表的方法提供了更好的可选择性,因此更适用于更大的representations;
- 提供了使用紧凑码的近邻图算法,并提供了基于邻居的量化回归,在十亿级数据集上取得最好效果。
如何近似一个向量?
获取一个向量的粗略近似的几种方式:
Centroid. 通过k-means聚类学习一个粗码本,可以在整个数据集上执行也可在一个有区分度的训练集上执行。我们可以通过一个向量在码本中最近的向量来近似该向量。
Nearest neighbor. 计算整个数据集上一个向量的最近邻居近似该向量。
Weighted average. 通过一个向量的k个最近向量的加权平均近似(权重向量$\beta^{\star}$是固定的)。
$$
\overline{x}=\beta ^{*T}N(x)
$$
Regression. 仍然通过$N(x)$近似x, 但权重$\beta$不再是固定的常数,而是与x有关的函数$\beta (x)$, 我们通过学习获取最优的回归系数$\beta (x)$以最小化x的重构误差
$$
\hat{x}=\beta (x) ^{T}N(x)
$$
其中$\beta (x)$通过对超定方程$||x-\beta (x) ^{T}N(x)||$进行最小二乘法求解获取。
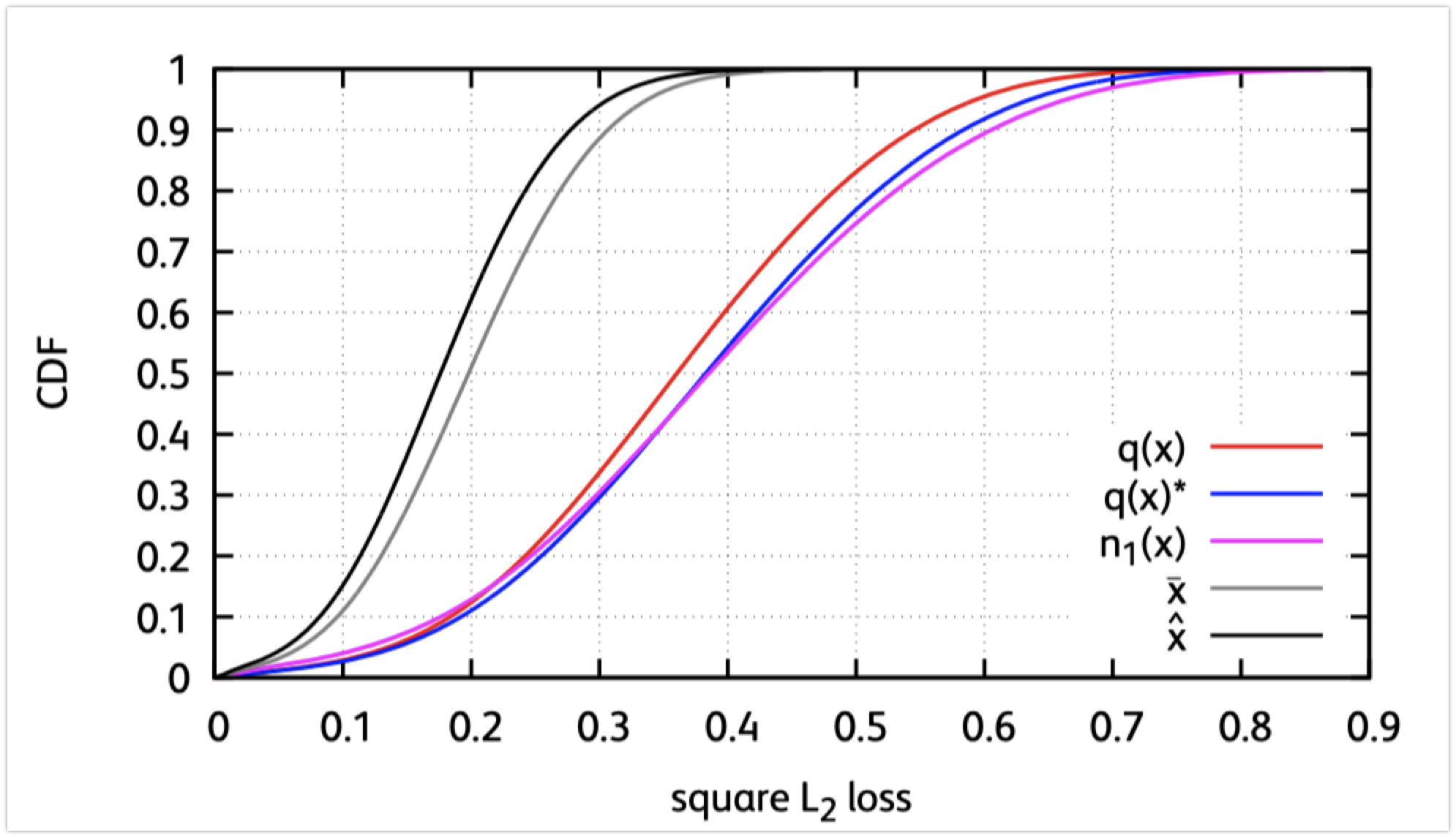
上图是对几种不同算法 的实验评估,横坐标为欧氏距离平方误差,纵坐标反映近似的质量。可见,centriod(q(x)是在原数据集上训练,q(x)*是在训练集上训练)比nearest neighbor(n1(x))近似的效果更好。
对$\overline{x}$而言,我们可以通过改进它的邻居(当前所有x共享同一个$\beta$)进一步提升近似;从$\hat{x}$可知,我们可以通过为每一个x设定一个不同的$\beta(x)$进一步提升近似.
本文提出的方法
Overview. 采用当前的方案将向量编码(2层编码,因为更好),与索引结构无关;采用HNSW结构,但是距离计算采用非对称距离计算(即查询或插入的新向量还是原始向量,索引中的向量采用编码向量);本文采用两种Refinement策略,主要用在下面的第二阶段。
搜索时是两阶段,第一阶段:通过量化编码获取一个候选集(索引向量仅通过紧凑码重构,即$q(x)$);第二阶段:在第一阶段获得的候选集上继续执行搜索(索引向量通过更精确的方案重构)。
方案一:
0-byte refinement (每个向量不需要额外存储自己的重构系数)
对于向量x (量化器编码$q(x)$),它的k个邻居为$g_{1}(x),\cdots,g_{k}(x)$,经量化器编码后,$q(g_{1}(x))$,$\cdots,q(g_{k}(x))$,构造一个矩阵
$$
\textbf{G}(x)=[q(x),q(g_1(x),\cdots,q(g_k(x)))]
$$
使用上面的矩阵重构一个更好的x,即在整个数据集$\mathcal{X}$上平方误差最小
$$
L(\beta)=\sum_{x \in \mathcal{X}}||x-\beta ^{T}\textbf{G}(x)||^2 \tag{1}
$$
对于
$$
\mathrm{X}=\left[\begin{array}{c}x_{1} \ \vdots \ x_{N}\end{array}\right],
\mathbf{Y}=\left[\begin{array}{c}\mathbf{G}\left(x_{1}\right) \ \vdots \ \mathbf{G}\left(x_{N}\right)\end{array}\right] \tag{2}
$$
上式对应数据集里面的所有x. (2)带入(1)得到矩阵方程$L(\beta)=\left|X-\beta^{\top} \mathbf{Y}\right|^{2}$,这是一个最小二乘问题,解得$L(\beta)$取最小对应$\beta^{\star}=\mathbf{Y}^{\star} X$, 其中$\mathbf{Y}^{*}$是$\mathbf{Y}$的摩尔彭若斯广义逆。
从而,我们可以通过$\overline{x}$较精确地估计x:
$$
\bar{x}=\beta^{\star^{\top}} \mathbf{G}(x)
$$
文中举了一个例子从侧面反映了通过上述方法比单纯通过$q(x)$估计x更准确:通过查看权重系数$\beta^{\star}$,当量化器较粗的时候,$q(x)$的权重是0.5, 当量化器较好的时候,$q(x)$的权重系数是0.9.
该方案操作起来比较简单,但是该方案对所有数据点采用无差别的重构系数,而不同的数据点的最优重构系数一般是不同的。
方案二:
regression codebook (每个向量有自己的重构系数,不过重构系数通过类似PQ的形式进行了编码)
如果每一个向量都有一个重构系数的话,存储重构系数会耗费大量的内存。因此,本文提出学习一个重构系数的码本$\mathcal{B}={\beta_{1}, \ldots, \beta_{B}}$, 以最小化下面的误差:
$$
L^{\prime}(\mathcal{B})=\sum_{x \in \mathcal{X}} \min _{\beta \in \mathcal{B}}\left|x-\beta^{\top} \mathbf{G}(x)\right|^{2}
$$
实际操作时,首先通过k-means初始化回归码本$\mathcal{B}$(在此之前可先得到每个向量的最优重构系数),然后执行以下步骤:
Step 1: 每个向量分配到使其重构误差最小的码字$\beta_{i}$中(即$\mathcal{B}$中的一个元素),从而每一个码字对应一些向量,这些向量通过该码字$\beta_{i}$对应的重构系数重构具有最小的重构误差。对应的公式为:
$$
\beta(x)=\arg \min_{\beta \in \mathcal{B}}||x-\beta^{\top} \mathbf{G}(x)||^{2}
$$
Step 2: 对每一个类$\beta_{i}$(或码字),通过下式计算最优重构系数$\beta_{i}^{\star}$(与公式(1)相同的方法)并以此更新该类的重构系数$\beta_{i} \leftarrow \beta_{i}^{\star}$
$$
\beta_{i}^{\star}=\arg \min_{\beta} \sum_{x \in \mathcal{X}: \beta(x)=\beta_{i}}||x-\beta^{\top} \mathbf{G}(x)||^{2}
$$
上述两步骤可迭代执行。实际操作时,需要$\mathcal{X}$的一个子集训练上述过程即可。
然而,随着码本尺寸的提升,上述过程很容易达到饱和,这主要因为:$\beta(x)^{\top} \mathbf{G}(x)$仅考虑了k+1维的子空间,$k \ll d$,因此x的有些部分无法恢复(或重构)。针对该问题,本文采用类似PQ的方案将向量划分为多个子空间,对每个子空间执行上述过程。
一些考虑
本文虽然是近邻图和量化编码的联合优势互补,但其整个论文是从如何更好进行数据近似这个角度撰写的,因此论文中主要从量化编码的角度讨论问题,可以说,近邻图是他们拿来降低量化编码误差的。

